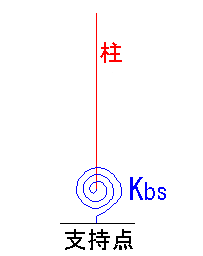
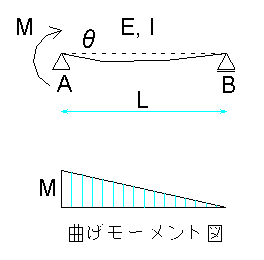A) この質問が意外と多いのでまとめて回答しておきます。弾性解析モード(FSA)を用いて次の要領でモデル化できます。
- 当該点のX,Y方向移動を拘束し、回転方向の移動を自由に設定する。
- 等価な回転剛性を持つ梁部材を接続する。
これを実現するには様々なモデルが考えられますが、ここでは1部材で、断面特性の入力データである断面2次モーメントに回転剛性の値を直接入力でき、汎用的に使用できる支持点モデルを設定します。
1) 回転バネ材に単純梁を用いる。
設定する回転剛性を Kbs (tonf*m/rad) とします。cm単位で表すと 100Kbs(tonf*cm/rad)となります。
柱脚を次の単純梁のA支点に接続すると、柱脚のモーメントMは剛結とした単純梁ABにて負担され、A支点には回転角θが発生します。ここでM/θが必要とするKbsとなるように、梁剛性(E, I, Lの関数)を決定すればよいのです。
2) この荷重状態の単純梁の支点Aの回転角と曲げモーメントの関係
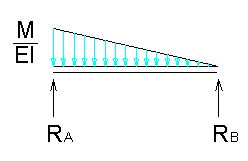
支持点Aの回転角は、モールの定理を用いると、上図の曲げモーメントの形状でM/EIを載荷した時のA点のせんだん力、すなわち、下図のRaとして求められます。
θa = Ra = M * L / ( 3 * E * I )
これより、回転剛性Kbsは次式で与えられることが分かります。
100Kbs = M /θa = 3EI / L
Kbsの値そのままを入力データの断面2次モーメント項に使用する、すなわち Kbs = I とするには、そのためには 3E / L = 100 の関係を保持してモデル化すればよいことになります。
弾性係数にはE = 2100[t/cm2] をそのまま使用すると、 L=63[cm]となります。
(注) 回転剛性をm系単位で与えるようにしたのは、cm系だと L=6300cm とする必要があり、モデル図が見づらくなるためです。
これで準備完了です。後は、どんな回転剛性の柱脚でも、
(1) 材長さ63cmの単純梁を接続し、
(2) 断面特性のE指定で、2100を指定、
(3) 断面特性のI指定で、回転剛性値を指定(ただし、単位は [tonf*m/rad] とする。)
することでモデル化が可能です。
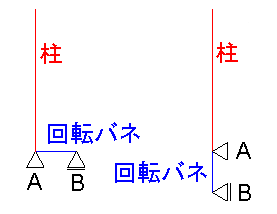
梁の方向はどちらを向いていようが構わないのですが、支持点反力を求める時には支持点A、Bの反力を合計する必要があるので、下図のように、水平あるいは鉛直に配置すればよいでしょう。
では、実際にモデル化をしてみましょう。 [FSAデータ]
柱□250x250x6、梁H294x200x8x12の1層1スパンフレームで中央に鉛直、水平の単位荷重が作用する2荷重ケースを想定しています。
柱脚の回転剛性は、ベースパック、ハイベースなどの製品毎に規定があるほか、アンカボルトをバネ材として伸び量から回転剛性を評価する方法などがありますが、ここでは、ベースパックのカタログから 柱□250x250x6用の 4700[tonf*m/rad] を採用します。回転剛性値が[tonf*cm/rad]で与えられている製品カタログでは 100 で除した値を使います。
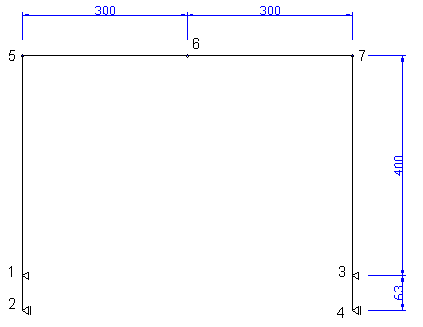
部材[1-2]、[3-4]が回転バネ材です。材長さは63cmとします。
JOIN
1 0 0
2 0 -63
3 600 0
4 600 -63
5 0 400
6 300 400
7 600 400
断面3が回転バネ材です。Iの項に回転剛性値をそのまま、Eの項に2100を指定します。A, Zは0でない任意値で構いません。
MEMB
1 57.63 5670 454 2100 0 0 'STKR250x250x6
2 71.05 11100 756 2100 0 0 'H294x200x8x12
3 100 4700 1000 2100 0 0 '回転柱脚
節点6に単位鉛直荷重が作用する場合の結果です。
節点 X-変位(cm) Y-変位(cm) 回転角(rad)
( 1) 0.000E+00 0.000E+00 3.956E-05
( 2) 0.000E+00 0.000E+00 -1.978E-05
( 3) 0.000E+00 0.000E+00 -3.956E-05
( 4) 0.000E+00 0.000E+00 1.978E-05
( 5) 3.166E-04 -1.653E-03 -3.938E-04
( 6) -1.134E-17 -1.090E-01 -3.959E-20
( 7) -3.166E-04 -1.653E-03 3.938E-04
【部材端力(部材座標系)】 N:引張を正、Q:時計回りを正、M:座標系は右手系
σmax=N/A+M/Z
部材 N(ton) Q(ton) Mi(ton・cm) Mj(ton・cm) σmax(ton/cm2)
{ 1} [ 1: 5] -5.000E-01 -1.575E-01 -1.860E+01 -4.440E+01 ( 0.11)
{ 2} [ 3: 7] -5.000E-01 1.575E-01 1.860E+01 4.440E+01 ( 0.11)
{ 3} [ 5: 6] -1.575E-01 5.000E-01 4.440E+01 1.056E+02 ( 0.14)
{ 4} [ 6: 7] -1.575E-01 -5.000E-01 -1.056E+02 -4.440E+01 ( 0.14)
{ 5} [ 1: 2] 0.000E+00 2.952E-01 1.860E+01 1.941E-15 ( 0.02)
{ 6} [ 3: 4] 0.000E+00 -2.952E-01 -1.860E+01 -5.117E-16 ( 0.02)
【支持点反力(全体座標系)】・・座標系は右手系
支持点 X方向(ton) Y方向(ton) モーメント(ton・cm)
( 1) 0.453 0.500 0.000
( 2) -0.295 0.000 0.000
( 3) -0.453 0.500 0.000
( 4) 0.295 0.000 0.000
------------------------------------------------------------
Sum 0.000 1.000
支持点反力の取り扱いだけ注意してください。単純梁の両支持点の反力合計が回転柱脚の反力となります。例えば左側の支持点は(1)(2)の合計で、X方向反力は0.158tonとなります。同様に右側支持点反力は-0.158tonです。
節点1の曲げモーメント1.860E+01を回転角3.956E-05で除した値が、設定した回転剛性と等しくなっていることを確認しておいてください。
次に回転剛性を設定できる他のソフトで検算してみましょう。
ここではH2XwinSIを使います。[H2Sデータ]
FOSSAPと合わせるためせんだん変形は無しで解析します。このソフトでは支持点のバネ条件をバネ定数(単位力を与えた時の変形量)で指定します。FOSSAPでは剛性(単位変形量を生じさせるための力)で与えるので、逆数(1/Kbs)となることに注意します。
添付データで、単位鉛直荷重が梁中央に作用する場合の解析結果は、
【節点変位】
節点 X方向変位 Y方向変位 回転角
(cm) (cm) (rad)
( 1) 0.0000 0.0000 0.000040
( 2) 0.0000 0.0000 -0.000040
( 3) 0.0003 -0.0017 -0.000394
( 4) 0.0000 -0.1090 0.000000
( 5) -0.0003 -0.0017 0.000394
【部材力】
部材 断面 節点 軸方向力 せん断力 モーメント 最大モーメント at
(ton) (ton) (ton*m) (ton*m) (m)
{ 1} 1/ 1 -0.500 -0.157 0.186
3 -0.500 -0.157 -0.444
{ 2} 1/ 2 -0.500 0.157 -0.186
5 -0.500 0.157 0.444
{ 3} 2/ 3 -0.157 0.500 -0.444
4 -0.157 0.500 1.056
{ 4} 2/ 4 -0.157 -0.500 1.056
5 -0.157 -0.500 -0.444
【支点反力】
支点 X方向 Y方向 モーメント
(ton) (ton) (ton*m)
( 1) 0.157 0.500 -0.186
( 2) -0.157 0.500 0.186
--------------------------------------------------
Sum 0.000 1.000
同じ結果が得られていることが確認できました。